B. Maximum Xor Secondary
Bike loves looking for the second maximum element in the sequence. The second maximum element in the sequence of distinct numbers x1, x2, ..., xk (k > 1) is such maximum element xj, that the following inequality holds: 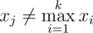 .
.
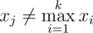 .
.
The lucky number of the sequence of distinct positive integers x1, x2, ..., xk (k > 1) is the number that is equal to the bitwise excluding OR of the maximum element of the sequence and the second maximum element of the sequence.
You've got a sequence of distinct positive integers s1, s2, ..., sn (n > 1). Let's denote sequence sl, sl + 1, ..., sr as s[l..r] (1 ≤ l < r ≤ n). Your task is to find the maximum number among all lucky numbers of sequences s[l..r].
Note that as all numbers in sequence s are distinct, all the given definitions make sence.
Input
The first line contains integer n (1 < n ≤ 105). The second line contains n distinct integers s1, s2, ..., sn (1 ≤ si ≤ 109).
Output
Print a single integer — the maximum lucky number among all lucky numbers of sequences s[l..r].
Sample test(s)
input
5 5 2 1 4 3
output
7
input
5 9 8 3 5 7
output
15
Note
For the first sample you can choose s[4..5] = {4, 3} and its lucky number is (4 xor 3) = 7. You can also choose s[1..2].
For the second sample you must choose s[2..5] = {8, 3, 5, 7}.
-------------------------------------------------------EDITORIAL--------------------------------------------------------------------
Brief Description
You’ve been given a sequence of distinct positive integers. Your task is to find a interval
[l, r], so that the maximum element xor the second maximum element within the interval is
as large as possible.
Analysis
The interval’s meaning can only be reflected on its maximum element and second maximum
element, so apparently, there must be a lot of meaningless interval which we needn’t
check them at all. But how can we skip them? Maintain a monotone-decreasing-stack
can help us. While a new element came into the view, pop the top element in the stack, and
check the corresponding interval, until the new element is greater than the top element in the
stack. We can easily see it is correct since we won’t lost the answer as long as it exists.
All the element at most push and pop once, and only been checked when popped. So the
time complexity turn to be O(N)
LETS SEE HOW ITS WORKING AND CHECKING ALL POSSIBILITY ..
LET ARRAY BE 1 3 2 5 6 4 9 10
if we consider all possible l and r , than all possible combinations of max ans 2nd max will be
(1,3) (3,2) (2,5) (3,5) ( 5,6) (6,4) (4,9) (6,9) (9,10)
now lets see how out monotonic decreasing stack check all these combinations.
we always maintain monotonic decreasing stack
1 push stack s<1,> stack
3 >1(top of stack pop till top()<3) update ans=max(ans,xor(1,3)) , pop 1 ,push 3, s<3>
2<3 update ans=max(ans,xor(2,3)) , push 2 s<3,2>
5 >2 update ans=max(ans, xor(2,5) pop(2), update ans=max(ans, xor(3,5) pop(3).. push(5) s<5>
similarly if u check all possible combination will be checked in o(2*n) since in the stack each element is pushed only once and pop only once ,
how it is working ....
in the range l to r only 1 max and 2nd max exists ,
now if we go for the range l to r+1, if that r+1 val change this max or 2nd max than only need to change else not , so we keep app monotonic decreasing elements is new element is < than the top element than for all sub string from 0 to r+1 it can form pair with the top element of the stack only(if possible ),
but if new val > top than it can form pair with all elements in the left which are of the top which is less than or 1st left element which is > this element ....
( think .... with the example than only it will give a clear understanding )
------------------------------------------------------code----------------------------------------------------------------------
#include<bits/stdc++.h>
using namespace std;
typedef long long int lli;
lli arr[1000000];
int main()
{
int n;
si(n);
for(int i=0;i<n;i++)
{
int a;
slli(arr[i]);
}
stack<lli> s;
lli ans=0;
for(int i=0;i<n;i++)
{
while(!s.empty())
{
if(s.top()<arr[i])
{
ans=max(ans,s.top() xor arr[i]);
s.pop();
}
else
{
ans=max(ans,s.top() xor arr[i]);
break;
}
}
s.push(arr[i]);
}
cout<<ans<<endl;
}